Adaptive Variable Selection for Sequential Prediction in Multivariate Dynamic Models by Mike West, Michael Lindon, and myself has been released on arXiv. In the paper, we discuss the advantages of comparing models using a specific objective function, rather than model likelihood. The need for well defined objectives is particularly clear in dynamic models, because in a time series setting, model likelihood is the product of 1-step forecast densities.
Given this perspective, we develop a strategy for dynamic variable selection in multivariate models. Models are scored with a synthetic Gibbs Probability based on an objective function, e.g. long term forecasting. We find groups of high scoring models near our current ‘best’ model, and forecast with a weighted combination of these models.
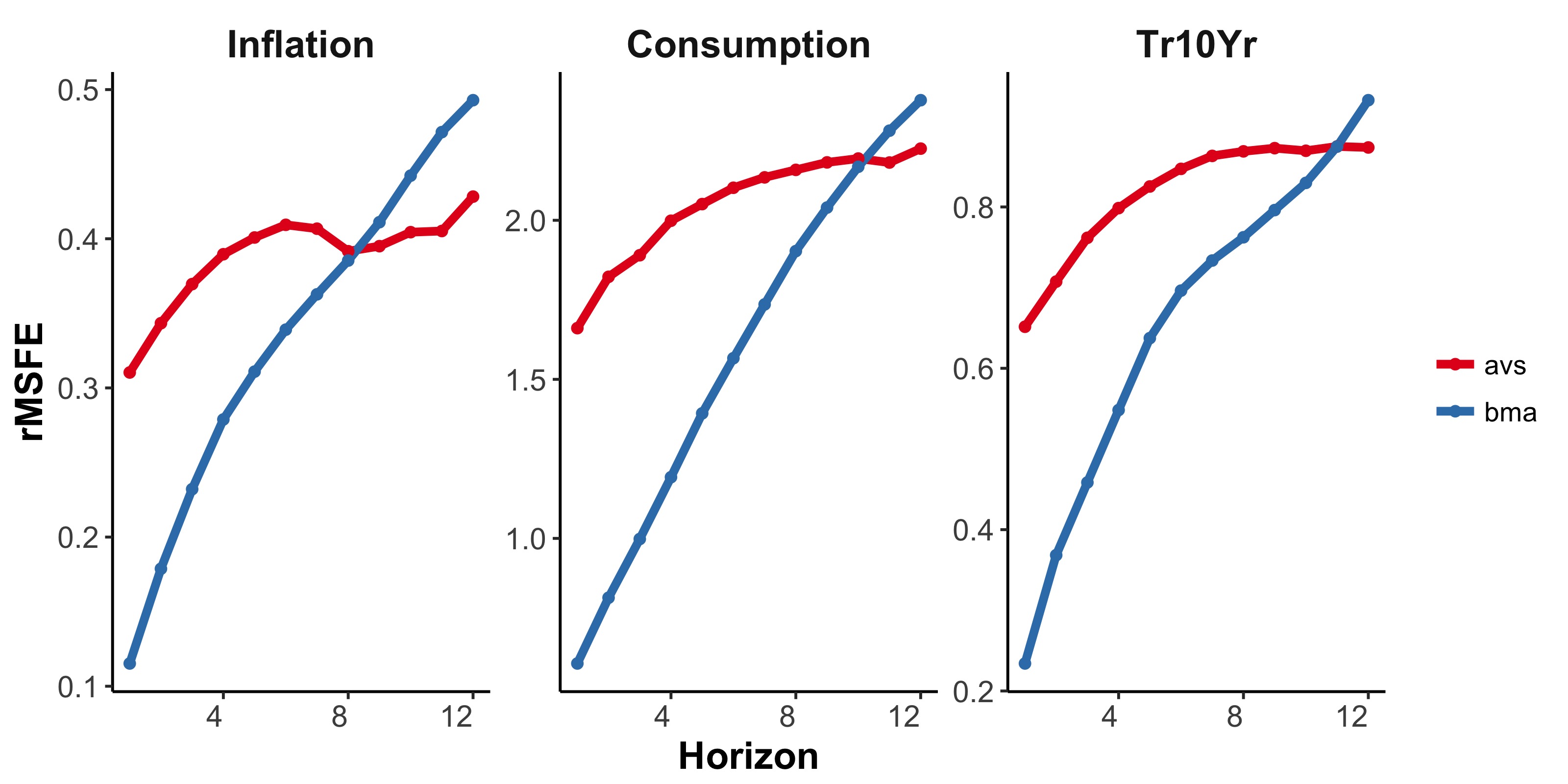
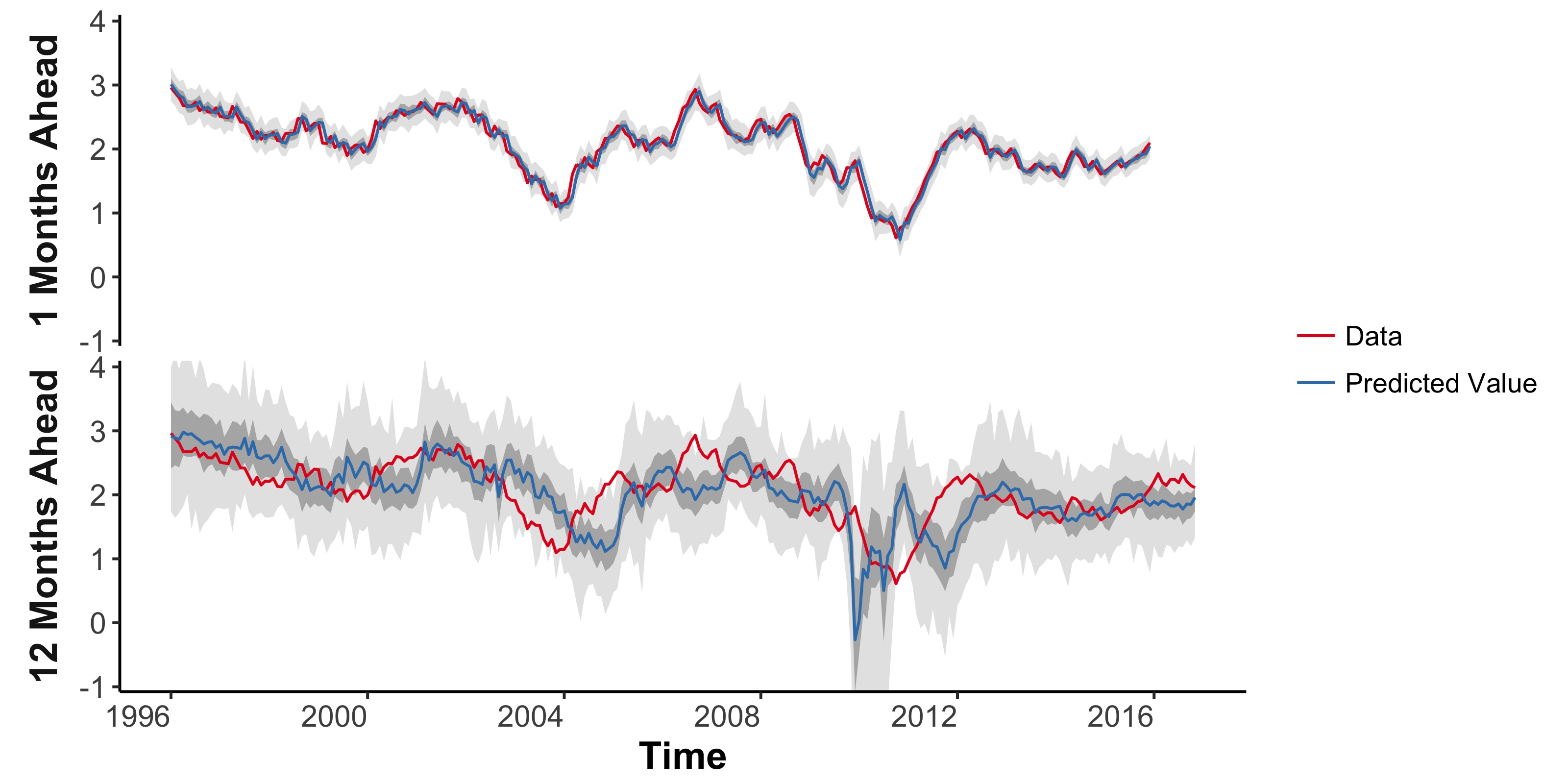
An example with 3 macroeconomic time series shows that using long term forecasting for model scores produces - as expected - far superior forecasts over long horizons than standard Bayesian model probabilities. The figure above shows the improved marginal forecast accuracy with model scores based on 12-month forecasts. We also consider using the joint 1-12 month forecast distribution (the path forecast distribution) as a model score. This produces models that balance their long and short term forecast accuracy. Shown below are forecasts of monthly US inflation with this score. The short term forecasts match those with Bayesian model probabilities, while the long term forecasts are more accurate.